स्टार कनेक्शन क्या होता है?

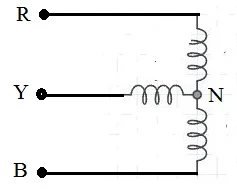
जब तीन कुंडली (Coil) या दुसरे कॉम्पोनेन्ट को इसप्रकार से आपस में जोड़ा जाता है की उसके तीन टर्मिनल आपस में एक दुसरे से एक बिंदु पर मिलते है तो ऐसे कनेक्शन को स्टार कनेक्शन कहा जाता है। जैसे की निचे के चित्र में दिखाया गया है। जिस बिंदु पर तीनो कुंडली आपस में मिलती ही उस बिंदु को न्यूट्रल बिंदु कहा जाता है। स्टार कनेक्शन का उपयोग हमेशा थ्री फेज पॉवर सिस्टम में किया जाता है। संतुलन की अवस्था की अवस्था में न्यूट्रल बिंदु का वोल्टेज शून्य वोल्ट होता है। इस चित्र में N न्यूट्रल बिंदु है।

डेल्टा कनेक्शन क्या होता है ?

तीन कुंडली को इस प्रकार से जोड़ा जाए की पहले कुंडली का दुसर टर्मिनल ,दुसरे कुंडली के पहले टर्मिनल से ,दुसरे कुंडली का दूसरा टर्मिनल तीसरे के पहले टर्मिनल से तथा तीसरे कुंडली का दूसरा टर्मिनल पहली कुंडली के पहले टर्मिनल से जुड़ा हो तब इस प्रकार के कनेक्शन को डेल्टा कनेक्शन कहा जाता है। जैसे की निचे के चित्र में दिखाया गया है। तीनो कुंडली इस प्रकार से जुड़कर एक बंद पास(Close loop) बनाती है। डेल्टा कनेक्शन में किसी भी प्रकार का न्यूट्रल पॉइंट नहीं होता है।

डेल्टा से स्टार में परिवर्तन (Delta to Star Conversion)

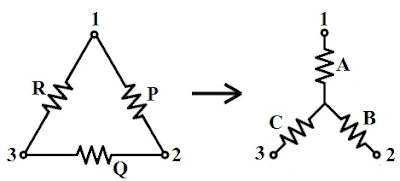
जब डेल्टा में जुड़े हुए प्रतिरोध को स्टार में परिवर्तित किया जाता है। तब स्टार कनेक्शन में जुड़े हुए प्रतिरोध का मान परिवर्तित हो जाता है। जिसे निम्न तरीके से ज्ञात किया जाता है :-

दोनों सर्किट के टर्मिनल 1 तथा 2 के बीच मौजूद प्रतिरोध को तुलना पर

P + Q = A तथा (B + C) समान्तर क्रम में जुड़े हुए है।

$P + Q =\frac{1}{\frac{1}{A} + \frac{1}{B+C} } =\frac{A(B+C)}{A+B+C}$

$P + Q =\frac{A(B+C)}{A+B+C}----(1)$

दोनों सर्किट के टर्मिनल 2 तथा 3 के बीच मौजूद प्रतिरोध को तुलना पर

R + Q = C तथा (B + A ) समान्तर क्रम में जुड़े हुए है।

ऊपर की तरह इसे सोल्व करने पर

$R + Q =\frac{C(B+A)}{A+B+C}----(2)$

दोनों सर्किट के टर्मिनल 1 तथा 3 के बीच मौजूद प्रतिरोध को तुलना पर

R + P = B तथा (C + A ) समान्तर क्रम में जुड़े हुए है।

ऊपर की तरह इसे सोल्व करने पर

$R + P =\frac{B(C+A)}{A+B+C}----(3)$

ऊपर दिए गए तीनो समीकरण को P ,Q तथा R के लिए हल करने पर

$P =\frac{AB}{A+B+C}$

$Q =\frac{AC}{A+B+C}$

$R =\frac{BC}{A+B+C}$

अर्थात जब डेल्टा में जुड़े हुए प्रतिरोध को उसके समतुल्य स्टार कनेक्शन में जोड़ा जाता है तब उसके प्रतिरोध का मान निम्न तरीके से बदल जाता है।

स्टार से डेल्टा में परिवर्तन ( Star to Delta Conversion)

स्टार को डेल्टा में बदलते समय ,डेल्टा के किसी भी ब्रांच का प्रतिरोध स्टार में जुड़े तीनो प्रतिरोध का दो दो के कॉम्बिनेशन के गुणनफल के योग तथा उसके सामने वाले प्रतिरोध के अनुपात के बराबर होता है। जैसे की निचे दिखाया गया है :-

डेल्टा में टर्मिनल 1 तथा 2 के बीच जुड़े हुए प्रतिरोध A का समतुल्य वैल्यू

$A =\frac{ PQ + QR+RP}{R}$