मैक्सवेल सेतु क्या है?
मैक्सवेल सेतु व्हीटस्टोन सेतु का मॉडिफाइड रूप है जिसमे किसी अज्ञात इंडक्टर (कॉइल) का Inductance ज्ञात किया जाता है। इस विधि में INDUCTANCE पहले से ज्ञात CAPACITANCE तथा INDUCTANCE के रूप में ज्ञात होता है। यह व्हीटस्टोन के संतुलन सिध्दांत पर कार्य करता है। इंडक्टर का प्रेरकत्व ज्ञात करने के लिए अन्य दूसरी विधिया भी है लेकिन मैक्सवेल सेतु विधुत उनमे सबसे ज्यादा उपयोग किए जाने वाली विधि है। किसी इंडक्टर के प्रेरकत्व को दो प्रकार के माक्सवेल सेतु से ज्ञात किया जाता है जिन्हें :
- मैक्सवेल प्रेरकत्व ब्रिज (Maxwell’s inductance bridge)
- मैक्सवेल प्रेरकत्व धारिता ब्रिज (Maxwell’s inductance capacitance bridge)
के नाम से जाना जाता है। मैक्सवेल सेतु को मैक्सवेल वेन सेतु भी कहा जाता है। मैक्सवेल सेतु एक प्रकार का ए०सी सेतु होता है।
मैक्सवेल प्रेरकत्व सेतु क्या होता है?
इस मैक्सवेल सेतु में अज्ञात कुंडली के प्रेरकत्व को एक ज्ञात प्रेरकत्व वाले कुंडली से तुलना कर ज्ञात किया जाता है। अर्थात इस सेतु से किसी अज्ञात कुंडली का प्रेरकत्व तथा आंतरिक प्रतिरोध को आसनी से ज्ञात किया जा सकता है। पहले से ज्ञात तथा अज्ञात कुंडली तथा प्रतिरोध को निचे दिखाए गए विधुत परिपथ के अनुसार जोड़ा जाता है।
जैसे ऊपर के परिपथ में दिखाया गया है कि विकर्ण B तथा D के बीच में एक गल्वेनोमीटर D को जोड़ा गया है जो इस विकर्ण से प्रवाहित होने वाली विधुत धारा को ज्ञात करेगा तथा परिवर्तनशील एवं ज्ञात प्रेरकत्व वाले कुंडली को भुजा AD और अज्ञात प्रेरकत्व वाले कुंडली को भुजा AB के बीच जोड़ा गया है। अन्य दो भुजाओ BC तथा CD के बीच पहले से ज्ञात प्रतिरोध(R3 R2) को जोड़ा गया है। एक प्रत्यावर्ती वोल्टेज श्रोत को विकर्ण AC के बीच जोड़ा गया है।
इस परिपथ में माना की
- अज्ञात कुंडली का प्रेरकत्व = L1
- अज्ञात कुंडली का आंतरिक प्रतिरोध = R1
- ज्ञात प्रतिरोध = R3 R2
- मानक परिवर्तनशील प्रतिरोध = R2
- मानक परिवर्तनशील कुंडली का प्रेरकत्व =L2
- मानक परिवर्तनशील कुंडली का आंतरिक प्रतिरोध =r2
ऊपर दिए गए परिपथ में विभिन्न भुजाओं के प्रतिबाधा को निम्न तरीके से लिखा जा सकता है।
जब उपर के परिपथ को प्रत्यावर्ती विधुत वोल्टेज श्रोत से जोड़ा जाता तब गैल्वनोमीटर से विधुत धारा का प्रवाह होने लगता है। परिवर्तनशील प्रतिरोध (R2) तथा कुंडली के प्रेरकत्व(L2) को समायोजित कर ,गेल्वनोमीटर से प्रवाहित होने वाली विधुत धारा को शून्य कर दिया है। विधुत परिपथ के इस दशा को संतुलन की अवस्था कहते है। व्हीटस्टोन सेतु के अनुसार संतुलन के अवस्था में
ऊपर के समीकरण में रियल तथा इमेजिनरी पार्ट को शून्य के बराबर करने पर
अतः अज्ञात कुंडली के प्रेरकत्व(L1) तथा आंतरिक प्रतिरोध(R1) को ज्ञात प्रतिरोध तथा प्रेरकत्व के रूप में व्यक्त किया जा सकता है।
मैक्सवेल प्रेरकत्व धारिता ब्रिज क्या है ?
इस मैक्सवेल सेतु में अज्ञात कुंडली के प्रेरकत्व को एक ज्ञात धारिता वाले कैपासिटर से तुलना कर ज्ञात किया जाता है। अर्थात इस सेतु से किसी अज्ञात कुंडली का प्रेरकत्व तथा आंतरिक प्रतिरोध को को मानक कैपासिटर से तुलना कर आसनी से ज्ञात किया जा सकता है। पहले से ज्ञात तथा अज्ञात कुंडली कैपासिटर तथा प्रतिरोध को निचे दिखाए गए विधुत परिपथ के अनुसार जोड़ा जाता है।
जैसे ऊपर के परिपथ में दिखाया गया है कि विकर्ण B तथा D के बीच में एक गल्वेनोमीटर D को जोड़ा गया है जो इस विकर्ण से प्रवाहित होने वाली विधुत धारा को ज्ञात करेगा तथा परिवर्तनशील एवं ज्ञात धारिता वाले कैपासिटर को भुजाCD और अज्ञात प्रेरकत्व वाले कुंडली को भुजा AB के बीच जोड़ा गया है। अन्य दो भुजाओ BC तथा AD के बीच पहले से ज्ञात प्रतिरोध(R3 R2) को जोड़ा गया है। एक प्रत्यावर्ती वोल्टेज श्रोत को विकर्ण AC के बीच जोड़ा गया है।
इस परिपथ में माना की
- अज्ञात कुंडली का प्रेरकत्व = L1
- अज्ञात कुंडली का आंतरिक प्रतिरोध = R1
- ज्ञात प्रतिरोध = R3 R2
- मानक परिवर्तनशील प्रतिरोध = R4
- मानक परिवर्तनशील कैपासिटर की धारिता =C4
ऊपर दिए गए परिपथ में विभिन्न भुजाओं के प्रतिबाधा को निम्न तरीके से लिखा जा सकता है।
जब उपर के परिपथ को प्रत्यावर्ती विधुत वोल्टेज श्रोत से जोड़ा जाता तब गैल्वनोमीटर से विधुत धारा का प्रवाह होने लगता है। परिवर्तनशील प्रतिरोध (R2) तथा कैपासिटर के धारिता (C4) को समायोजित कर ,गेल्वनोमीटर से प्रवाहित होने वाली विधुत धारा को शून्य कर दिया है। विधुत परिपथ के इस दशा को संतुलन की अवस्था कहते है। व्हीटस्टोन सेतु के अनुसार संतुलन के अवस्था में
मैक्सवेल ब्रिज उपयोग के लाभ एवं हानि
कुंडली के प्रेरकत्व ज्ञात करने में मैक्सवेल ब्रिज के निम्न लाभ एवं हानि है :-
लाभ
- मैक्सवेल सेतु से प्राप्त समीकरण में फ्रीक्वेंसी का कोई रोल नहीं होता है।
- प्रतिरोध तथा प्रेरकत्व के लिए प्राप्त दोनों समीकरण एक दुसरे से स्वतंत्र है।
- इस सेतु के मदद से उच्च मान वाले कुंडली के प्रेरकत्व को आसनी से ज्ञात किया जा सकता है।
हानि
परिवर्तनशील कैपासिटर के उपयोग से यह महंगा हो जाता है।
यह 1 तथा 10 बीच क्वालिटी वाले कुंडली के लिए ही ठीक है।



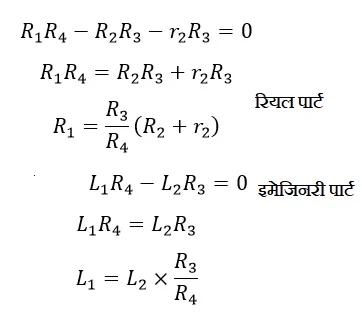




एक टिप्पणी भेजें
एक टिप्पणी भेजें