प्रत्यावर्ती विधुत परिपथ में कालांतर क्या होता है?
किसी परिपथ में प्रत्यावर्ती वोल्टेज का श्रोत जोड़ देने पर परिपथ में प्रवाहित होने वाली विधुत धारा की आवृति हमेशा प्रत्यावर्ती वोल्टेज के आवृति के बराबर होती है लेकिन यह जरुरी नही है की विधुत धारा तथा वोल्टेज दोनों एक साथ परिपथ में अपने अधिकतम मान अर्थात शिखर मान को प्राप्त करे। विधुत परिपथ में ऐसा हो सकता है की दोनों में से कोई राशि अपने शिखर मान को पहले प्राप्त करे तथा दूसरी राशि अपने शिखर मान को थोड़ी देर बात प्राप्त करे। विधुत धारा तथा वोल्टेज में उत्पन्न हुए इस अंतर को ही कालांतर कहते है। जिसे अंग्रेजी में Phase Difference कहा जाता है। जब वोल्टेज तथा विधुत धारा दोनों एक साथ अपने अधिकतम तथा न्यूनतम मान को प्राप्त`करते है तब उन्हें एक ही कला में कहा जाता है। वोल्टेज या करंट में उत्पन्न इस प्रकार के अंतर को अग्रगामी(Leading) या पश्चगामी(Lagging) कहा जाता है। किसी परिपथ में प्र्वाहित हो रही विधुत धारा तथा वोल्टेज से संबंधित तीन परिस्थतिया बन सकती है और इन तीनो परिस्थिति को समीकरण तथा ग्राप से दिखाया जा सकता है जो निम्न है :-
जब वोल्टेज तथा विधुत धारा दोनों एक साथ अपने अधिकतम मान (शिखर मान) को प्राप्त करे
इस परिस्थिति में जब वोल्टेज तथा विधुत धारा दोनों एक साथ अपने शिखर मान को प्राप्त करते है तब इनको निम्न तरीके से समीकरण तथा ग्राफ के रूप में दिखाया जाता है
ऊपर लिखित समीकरण से ज्ञात होता है कि दोनों वोल्टेज तथा करंट ज्या वक्रीय है इसलिए इनका ग्राफ निम्न होगा 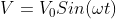

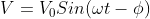
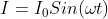 कभी कभी ऐसा होता है की वोल्टेज विधुत धारा से पहले ही अपने शिखर मान को प्राप्त कर लेता है। ऐसी परिस्थिति में विधुत धारा पश्चगामी (Lagging Current) कहलाती है। ऐसी घटना Inductive लोड वाले सर्किट में देखने को मिलता है। चूँकि वोल्टेज, करंट से आगे चलता है इसलिए इसके समीकरण में फेज कोण में फाई (𝝓)कोण जोड़ दिया जाता है। या करंट समीकरण के फेज से (𝝓)कोण घटा लिया जाता है। फाई का मान सर्किट में जुड़े हुए लोड के परिमाण पर निर्भर करता है। जैसे
कभी कभी ऐसा होता है की वोल्टेज विधुत धारा से पहले ही अपने शिखर मान को प्राप्त कर लेता है। ऐसी परिस्थिति में विधुत धारा पश्चगामी (Lagging Current) कहलाती है। ऐसी घटना Inductive लोड वाले सर्किट में देखने को मिलता है। चूँकि वोल्टेज, करंट से आगे चलता है इसलिए इसके समीकरण में फेज कोण में फाई (𝝓)कोण जोड़ दिया जाता है। या करंट समीकरण के फेज से (𝝓)कोण घटा लिया जाता है। फाई का मान सर्किट में जुड़े हुए लोड के परिमाण पर निर्भर करता है। जैसे
जब परिपथ में धारा का मान वोल्टेज से पहले ही शिखर मान को प्राप्त कर ले
कभी कभी ऐसा भी होता है की विधुत धारा वोल्टेज से पहले ही अपने शिखर मान को प्राप्त कर लेता है। ऐसी परिस्थिति में विधुत धारा अग्रगामी कहलाती है। ऐसी घटना Capacitive लोड वाले सर्किट में देखने को मिलता है। चूँकि करंट वोल्टेज से आगे चलता है इसलिए इसके समीकरण में फेज कोण में फाई (𝝓)कोण जोड़ दिया जाता है। या वोल्टेज समीकरण के फेज से (𝝓)कोण घटा लिया जाता है। फाई का मान सर्किट में जुड़े हुए लोड के परिमाण पर निर्भर करता है। जैसे
या
इन दोनों समीकरण को ग्राफ के मदद से निम्न तरीके से दिखाया जा सकता है
जब परिपथ में वोल्टेज का मान करंट से पहले ही शिखर मान को प्राप्त कर ले
या
इन दोनों समीकरण को ग्राफ के मदद से निम्न तरीके से दिखाया जा सकता है



एक टिप्पणी भेजें
एक टिप्पणी भेजें