Active ,Reactive and Apparent Power In Hindi

प्रत्यावर्ती वोल्टेज तथा प्रत्यावर्ती धारा कैसे उत्पन्न होती है ?

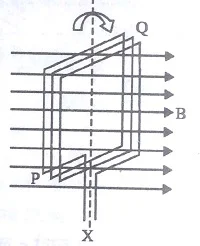
जब आयताकार या वृताकार कुंडली (Coil) को चुंबकीय क्षेत्र में तेजी से घुमाया जाता है तो कुंडली से होकर गुजरने वाली चुंबकीय बल रेखाए अर्थात कुंडली से सम्बंधित चुंबकीय फ्लक्स में लगातार परिवर्तन होता रहता है। फ्लक्स में इस प्रकार होने वाली परिवर्तन की वजह से फैराडे के नियमानुसार कुंडली के दोनों टर्मिनल के बीच एक EMF उत्पन्न हो जाता है। यदि कुंडली को किसी बाहरी परिपथ से जोड़ा जाए तब परिपथ में एक विधुत धारा का प्रवाह होने लगता है। कुंडली में प्रेरित इस विधुत धारा की दिशा को फ्लेमिंग के दाए हाथ के नियम से ज्ञात किया जा सकता है। कुंडली को घुमाने में किया गया कार्य ही विधुत ऊर्जा के रूप में प्राप्त होता है। निचे दिए गए चित्र में एक आयताकार कुंडली को एक चुंबकीय क्षेत्र में घूमते हुए दिखाया गया है। 

माना की चुंबकीय फ्लक्स का घनत्व B है तथा इसकी दिशा कुंडली के क्षेत्रफल के लंबवत है। कुंडली उर्ध्वाधर अक्ष  (Vertical Axis) के परितः क्लॉक वाइज घूम रही है। माना की कुंडली का कुल क्षेत्रफल क्षेत्रफल A तथा इसमें कुल फेरो की संख्या N है। चूँकि कुंडली घूम रही है इसलिए प्रत्येक क्षण इसकी दिशा चुंबकीय फ्लक्स से बदल रही है इसलिए मान लेते है की किसी क्षण कुंडली चुंबकीय क्षेत्र B से θ कोण बना रहा है। जैस की निचे के चित्र में दिखाया गाया है। 

 इस क्षण चुंबकीय क्षेत्र B का कुंडली के तल के लंबवत दिशा में कॉम्पोनेन्ट BCosθ  होगा इसलिए इस वक्त कुंडली से सम्बंधित कुल चुंबकीय फ्लक्स (𝛗 )को निम्न तरीके से व्यक्त किया जा सकता है। 

𝛗 = N x (BCosθ)x A 

𝛗 = NBA Cosθ

यदि कुंडली नियत कोणीय वेग ω से घूम रही हो तब 

θ = ωt 

𝛗 = NBA Cos(ωt)

फ्लक्स परिवर्तन की दर = E

फैराडे के विधुत चुंबकीय प्रेरण  सिध्दांत  से कुंडली में प्रेरित EMF उससे संबंधित चुंबकीय फ्लक्स में परिवर्तन के ऋणात्मक दर के बराबर होता है अर्थात 

यदि 

यह किसी कुंडली में उत्पन्न वोल्टेज का समीकरण है जो प्रत्यावर्ती  रूप से बदलता रहता है इसलिए  अंग्रेजी में Alternating Voltage (AC वोल्टेज )  कहा जाता है। यदि उपर के समीकरण में EMF को V से Replace कर दिया जाए तब यह समीकरण कुछ ऐसा होगा 

इस वोल्टेज समीकरण से ज्ञात होता है की जब किसी कुंडली को किसी चुम्बकीय क्षेत्र में घुमाया जाता है तब उसमे प्रेरित EMF ज्या वक्र की भाति बदलता रहता है। 

चूँकि वोल्टेज समीकरण समय का फलन है इसलिए इसका परिमाण तथा दिशा समय के साथ बदलता रहेगा। समय के अलग अलग अलग क्षण पर इसका परिमाण तथा दिशा अलग अलग होगा। अर्थात 

ऐसी वोल्टता को जो परिमाण तथा दिशा में समय के साथ आवर्त रूप से बदलती हो अर्थात एक निश्चित समय के बाद उसी दिशा में उसी परिमाण के साथ उसकी पुरावृति होती हो उसे प्रत्यावर्ती वोल्टता कहते है। 

प्रत्यावर्ती विधुत धारा क्या होती है ? 

कुंडली में उत्पन्न प्रत्यावर्ती  वोल्टेज को जब किसी बाहरी विधुत परिपथ से जोड़ा जाता है तब उस परिपथ में एक विधुत धारा का प्रवाह होने लगता है जिसकी प्रकृति वोल्टेज के सामान ही होता है। यदि वोल्टेज ज्या वक्रीय है तब विधुत धारा भी ज्या वक्रीय होगी है। यदि प्रवाहित होने वाली विधुत धारा I हो तब इसे समीकरण के रूप में ऐसे लिखा जा सकता है 

यह भी पढ़े 

पीक फैक्टर तथा फॉर्म फैक्टर क्या होता है?

पॉवर फैक्टर क्या होता है?

एक्टिव पॉवर क्या होता है ?