प्रत्यावर्ती विधुत धारा किसे कहते है ?

ऐसी विधुत धारा जिसका परिमाण तथा दिशा आवर्त रूप से बदलता रहे उसे प्रत्यावर्ती विधुत धारा कहते है। प्रत्यावर्ती विधुत धारा को एम्पियर में मापा जाता है। यह एक सदिश राशि है। प्रत्यावर्ती धारा को पूर्ण रूप से समझने के लिए उससे सम्बंधित निम्न बातो की जानकारी होना आवश्यक है :

विधुत धारा का आयाम
विधुत धारा की आवृति
विधुत धारा RMS मान
विधुत धारा का औसत मान

आयाम क्या होता है?

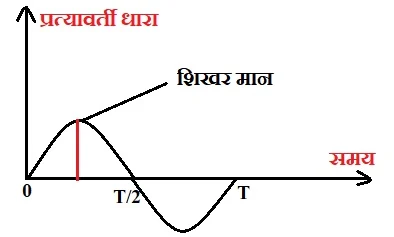
चुम्बकीय क्षेत्र में घुमती हुई कुंडली की दो स्थितियों में परिपथ में उत्पन्न प्रत्यावर्ती धारा का मान अधिकतम होता है। प्रत्यावर्ती धारा के इस अधिकतम मान को ही उसका आयाम या शिखर मान कहते है। इसे अंग्रेजी में Amplitude कहा जाता है। इसे से प्रदर्शित किया जाता है। इसे दिए गए ग्राफ में दिखाया गया है।

आवर्त काल क्या होता है ?

जितने समय में चुंबकीय क्षेत्र में घुमती हुई कुंडली एक चक्कर पूरा करती है ,ठीक उतने ही समय में कुंडली से जुड़े परिपथ में प्रत्यावर्ती धारा पहले एक दिशा में शून्य से अधिकतम तथा अधिकतम से शून्य हो जाती है। इसे विधुत धारा का एक चक्र कहते है। प्रत्यावर्ती धारा द्वारा एक चक्र पूरा करने में जो समय लगता या व्यतित होता है उस समय को ही विधुत धारा का आवर्त काल कहा जाता है। इसे अंग्रेजी में Time Period कहा जाता है। इसे T से सूचित किया जाता है।

आवर्त काल = कुंडली के एक चक्कर घुमने में लगा हुआ समय

यदि कुंडली का कोणीय वेग (ω) हो तब इसे एक चक्कर पूरा करने में लगे हुए समय (T) को निम्न तरीके से व्यक्त किया जा सकता है।

$T = \frac{2\pi }{\omega }$

आवृति क्या होता है ?

प्रत्यावर्ती विधुत धारा द्वारा एक सेकंड में जितने चक्र (Cycle) लगाया जाता है उसे प्रत्यावर्ती धारा का आवर्त आवृति कहते है। इसका मान कुंडली द्वारा एक सेकंड में लगाये गए कुल चक्करों की संख्या के बराबर होता है। यदि प्रत्यावर्ती धारा का आवर्त काल T हो तो आवृति f को निम्न तरीके से ज्ञात किया जा सकता है

$f= \frac{1}{T}$

जबकि

$T = \frac{2\pi }{\omega }$

तब आवृति f को कोणीय वेग के रूप में निम्न तरीके से व्यक्त किया जा सकता है

$f = \frac{\omega }{2\pi }$

आवृति का मात्रक साइकिल प्रति सेकंड (cps)होता है जिसे हेर्ट्ज़ (Hz) कहा जाता है। हमारे घरो में उपयोग की जाने वाली विधुत धारा की आवृति 50 हर्ट्ज़ होती है।

प्रत्यावर्ती धारा का औसत मान क्या होता है ?

प्रत्यावर्ती विधुत धारा पुरे एक चक्र के दौरान आधे चक्र में एक दिशा में तथा दुसरे आधे चक्र में विपरीत दिशा में अधिकतम मान (शिखर मान) को प्राप्त करती है। अतः पुरे एक चक्र के दौरान विधुत धारा का औसत मान शून्य होगा। इसलिए प्रत्यावर्ती विधुत धारा के आधे धनात्मक चक्र के लिय विधुत धारा का औसत मान ज्ञात किया जाता है। माना की किसी क्षण प्रत्यावर्ती विधुत धारा का तात्कालिक मान निम्न है।

$I= I_{0}Sin(\omega t)$