Active ,Reactive and Apparent Power In Hindi

 मैक्सवेल का लूप नियम क्या है?

यह नियम किसी जटिल विधुत परिपथ के विभिन्न लूप में प्रवाहित होने वाली सभी विधुत धाराओ के बीच संबंध स्थापित करता है जिसके मदद से लूप तथा अन्य दुसरे ब्रांच में प्रवाहित होने वाली विधुत धारा का परिमाण ज्ञात किया जाता है। परिपथ में जितने भी लूप होते है उन सभी लूप में एक स्वतंत्र विधुत धारा का प्रवाह होता है। जटिल परिपथ में जितने लूप की संख्या होती है उतने वेरिएबल के रैखिक समीकरण होती है तथा इन सभी रैखिक समीकरण को हल करने से प्रत्येक लूप से सम्बंधित विधुत धारा का परिमाण ज्ञात होता है। मैक्सवेल का यह नियम डीसी तथा एoसी दोनों प्रकार के परिपथ से लिए बराबर सही है। इसे समझने के लिए हम एक परिपथ का सहारा लेते है जिसमे तीन लूप है तथा जिसमे दो विधुत उर्जा श्रोत जुड़े हुए है।  

जैसे की ऊपर विधुत परिपथ में दिखाया गया है की प्रत्येक लूप में एक विधुत धारा का प्रवाह हो रहा है। चूँकि परिपथ में कुल लूप की संख्या तीन है अतः तीनो लूप में  प्रवाहित होने वाली विधुत धारा के परिमाण को ज्ञात करने के लिए कुल तीन रैखिक समीकरण बनेंगे जो तीनो विधुत धारा को आपस में सम्बंधित करेंगे। 

पहला लूप में  

E1 – I1R – R4 (I1 – I2) = 0

I1 (R1 + R4) – I2R4 – E1 = 0

I1 (R1 + R4) – I2R4 = E1 --------(1)

दूसरा  लूप में  

-I2R2 – R5 (I2 – I3) – R4 (I2 – I1) = 0
I1R4 – I2 (R2 + R4 + R5) + I3R5 = 0----(2)

तीसरे  लूप में  

 - I3R3 – E2 – R5 (I3 – I2) = 0
 I2R5 – I3 (R3 + R5) = E2 ----(3)

तीनो लूप से प्राप्त समीकरण -1 ,2 तथा समीकरण -3 को हल करने पर तीनो लूप में प्रवाहित होने वाली विधुत धारा का परिमाण प्राप्त होता है। 

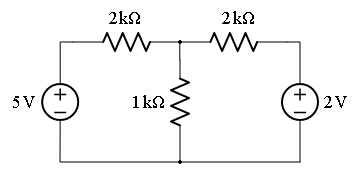
उदहारण : निचे दिए गए परिपथ के प्रत्येक लूप में प्रवाहित होने वाली विधुत धारा का परिमाण ज्ञात करे। 

ऊपर दिए गए विधुत परिपथ में  कुल दो वोल्टेज श्रोत जुड़े हुए है और परिपथ में कुल लूप की संख्या 2 है। अतः कुल दो समीकरण प्राप्त होंगे जिसे हल करने के बाद  प्रत्येक लूप से प्रवाहित होने वाली विधुत धारा का परिमाण प्राप्त होगा। 

माना की लूप -1 में प्रवाहित विधुत धारा I_i है तथा लूप-2 में प्रवाहित विधुत धारा I_ii है। लूप -1 तथा लूप-2 में 1KΩ उभयनिष्ट है। अतः इसमें प्रवाहित होने वाली विधुत धारा का परिमाण दोनों लूप में प्रवाहित होने वाली विधुत धारा के योग या अंतर के बराबर होगा। 

लूप-1 में 

+5V−2000iI​−1000(iI​−iII​)

−2000iI​−1000iI​+1000iII​=−5------(1)

लूप -2 में 

+1000(iI​−iII​)−2000iII​−2V=0

+1000iI​−1000iII​−2000iII​=+2-----(2)

ऊपर दिए गए दोनों समीकरण को हल करने पर 

iI​=+1.625mA

iI​=-0.125mA

यह भी पढ़े 

थर्मोकपल क्या होता है ?

मेगर कैसे कार्य करता है ? 

टिडल ऊर्जा क्या होती है ?

कूलम्ब का नियम क्या है?

तीन वाटमीटर द्वारा विधुत ऊर्जा को कैसे मापा जाता है?