Active ,Reactive and Apparent Power In Hindi

 त्रिभुज क्या होता है?

त्रिभुज (triangle)तीन रेखाओ द्वारा घिरा हुआ एक दो विमीय(two dimensional) आकृति होता है। दो विमीय से हमारा अभिप्राय यह केवल दो तल में ही बनाया जा सकता है। त्रिभुज को कभी भी तीन तल में नहीं बनाया जा सकता है। एक एक बहुत ही महत्वपूर्ण आकृति होता है। जमीन संबंधित गणना में त्रिभुजाकार आकृति से मिलता जुलता बहुत से प्लाट पाए जाते है उन सभी प्लाट का क्षेत्रफल ज्ञात करने के लिए त्रिभुज से सम्बंधित सूत्र की आवश्यकता होती है।  इस लेख में त्रिभुज से सम्बंधित सभी प्रकार के सूत्र की व्याख्या किया जायेगा। 

त्रिभुज का परिमाप क्या होता है?

त्रिभुज के परिमाप से हमारा अभिप्राय इसके तीनो भुजाओ के लम्बाई के योग से होता है। परिमाप त्रिभुज से सम्बंधित एक बहुत ही महत्वपूर्ण पैरामीटर होता है।  इसे अंग्रेजी में Premeter कहा जाता है। किसी भी त्रिभुज का परिमाप इसके तीनो भुजाओ के लम्बाई के योग के बराबर होता है। त्रिभुज के लम्बाई की गणना उस वक्त किया जाता है जब किसी त्रिभुजाकार आकृति के चारो तरफ घेरने के लिए रस्सी या बास (Bamboos) की जरुरत पड़ती है। जैसे यदि किसी त्रिभुजाकार प्लाट को बांस से घेरना है। तब इसको घेरने के लिए बांस की लम्बाई कितनी होगी। ऐसे स्थिति में घेरने के लिए लगाये गए कुल बांस की लम्बाई उस त्रिभुजाकार प्लाट के तीनो भुजाओ के योग के बराबर अर्थात त्रिभुज के परिमाप के बराबर होगी। 

यदि

परिमाप = P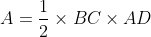

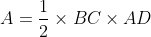
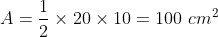
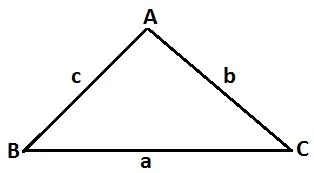
भुजा BC = a

भुजा AC = b

भुजा AB = c

त्रिभुज के परिमाप = तीनो भुजाओ का योग 

त्रिभुज के परिमाप = AB + BC +AC

चूँकि परिमाप भुजाओ के लम्बाई का योग होता है इसलिए इसलिए इसे हमेशा मीटर (m),सेंटीमीटर (cm) आदि में मापा जाता है। 

त्रिभुज का क्षेत्रफल क्या होता है?

त्रिभुज का क्षेत्रफल इसके तीनो भुजाओ के बीच घिरे हुए क्षेत्र को कहते है। किसी भी त्रिभुज द्वारा घेरा गया क्षेत्र उसके भुजाओ के लम्बाई के समानुपाती होता है। अर्थात तत्रिभुज के भुजाओ की लम्बाई जितनी ज्यादा होगी उसका क्षेत्रफल भी उतना ही ज्यादा होता है। किसी भी त्रिभुज का क्षेत्रफल उसके आधार तथा संगत उचाई के गुणनफल का आधा(Half) होता है। 

त्रिभुज के क्षेत्रफल = (1/2 )x आधार x उच्चाई 

दिए चित्र के अनुसार 

आधार = BC 

उच्चाई = AD 

यदि त्रिभुज के क्षेत्रफल =  A 

यह त्रिभुज के क्षेत्रफल ज्ञात करने का सर्वव्यापी फार्मूला है। 

उदहारण : यदि किसी त्रिभुज की सांगत उच्चाई 10 cm तथा इसके आधार की लम्बाई 20 cm है तब इसका क्षेत्रफल कितना होगा। 

इस प्रश्न में दिया गया है :-

त्रिभुज की उचाई =  AD = 10 cm 

आधार की लम्बाई = BC = 20 cm 

माना की त्रिभुज का क्षेत्रफल = A 

अतः इस त्रिभुज का क्षेत्रफल = 100 वर्ग सेमी होगा। 

त्रिभुज कितने प्रकार के होते है?

त्रिभुज के भुजाओ के लम्बाई के आधार पर ,इसे तीन वर्गों में वर्गीकृत किया जाता है। ये तीन प्रकार के त्रिभुज निम्न है :-

विषम बाहूत्रिभुज (Sclene Triangle)

समद्विबाहु त्रिभुज (Isosceles triangle)

समबाहु त्रिभुज (Equilateral Triangle)